Geodesic polar coordinates
According to @needham2021visual page 274, they are the generalization to an arbitrary surface of the idea of spherical coordinates on $\mathbb{S}^2$.
If we imagine great circles departing from the north pole in every direction with unit speed, then every point on $\mathbb{S}^2$ is characterized by which particle hits this point (labelled by the longitude $\theta$), and when (specified by the latitude $\phi=t$).
Well, that idea in an arbitrary surface are geodesics polar coordinates $(t,\theta)$.
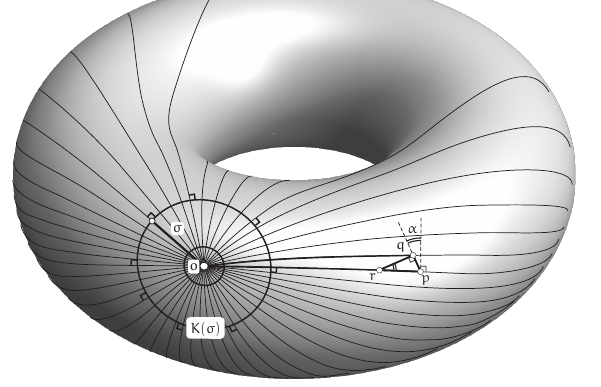
An important result is Gauss lemma.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: